1901. Find a Peak Element II

Problem Link

Description

---

A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.

Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].

You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.

You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.

 

Example 1:

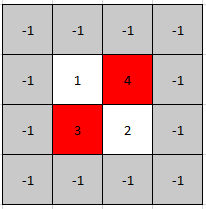
Input: mat = [[1,4],[3,2]]
Output: [0,1]
Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.

Example 2:

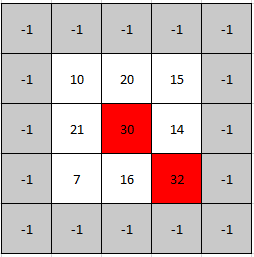
Input: mat = [[10,20,15],[21,30,14],[7,16,32]]
Output: [1,1]
Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 105
• No two adjacent cells are equal.

Solution

---

Python3

class Solution:
    def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
        rows, cols = len(mat), len(mat[0])
        
        top = 0
        bottom = rows - 1
        
        while bottom > top:
            mid = (top + bottom) // 2
            if max(mat[mid]) > max(mat[mid+1]):
                bottom = mid
            else:
                top = mid + 1
                
        return [bottom, mat[bottom].index(max(mat[bottom]))]