Description
You are given an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
You are also given a 0-indexed integer array cost of length n, where cost[i] is the cost assigned to the ith node.
You need to place some coins on every node of the tree. The number of coins to be placed at node i can be calculated as:
- If size of the subtree of node
iis less than3, place1coin. - Otherwise, place an amount of coins equal to the maximum product of cost values assigned to
3distinct nodes in the subtree of nodei. If this product is negative, place0coins.
Return an array coin of size n such that coin[i] is the number of coins placed at node i.
Example 1:
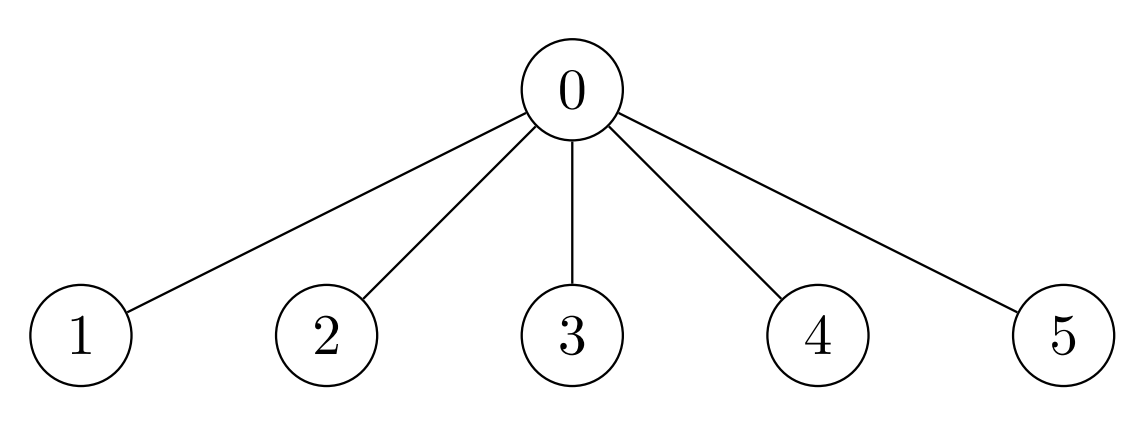
Input: edges = [[0,1],[0,2],[0,3],[0,4],[0,5]], cost = [1,2,3,4,5,6] Output: [120,1,1,1,1,1] Explanation: For node 0 place 6 * 5 * 4 = 120 coins. All other nodes are leaves with subtree of size 1, place 1 coin on each of them.
Example 2:
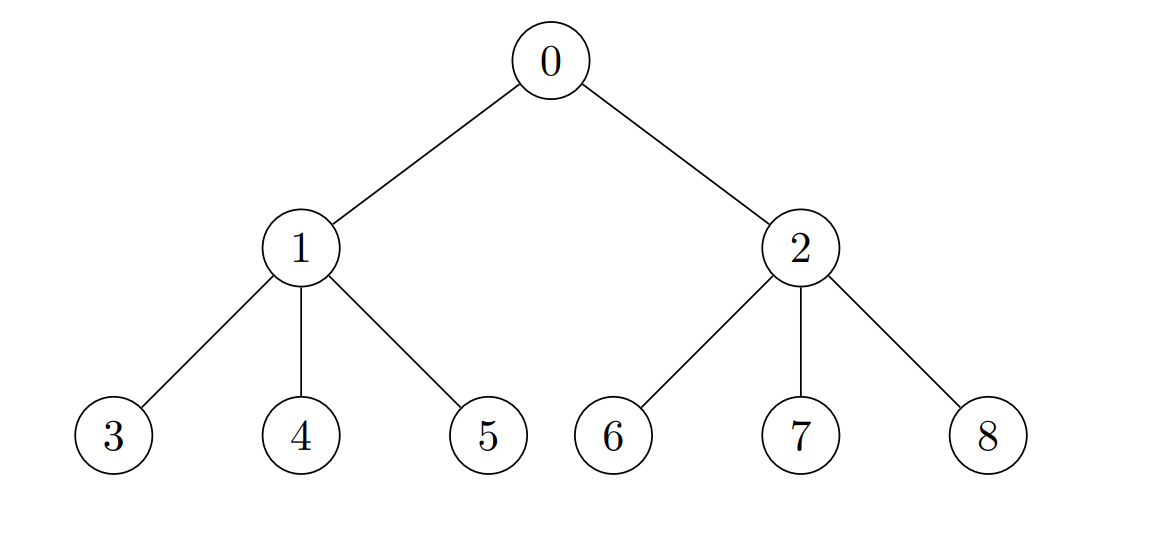
Input: edges = [[0,1],[0,2],[1,3],[1,4],[1,5],[2,6],[2,7],[2,8]], cost = [1,4,2,3,5,7,8,-4,2] Output: [280,140,32,1,1,1,1,1,1] Explanation: The coins placed on each node are: - Place 8 * 7 * 5 = 280 coins on node 0. - Place 7 * 5 * 4 = 140 coins on node 1. - Place 8 * 2 * 2 = 32 coins on node 2. - All other nodes are leaves with subtree of size 1, place 1 coin on each of them.
Example 3:
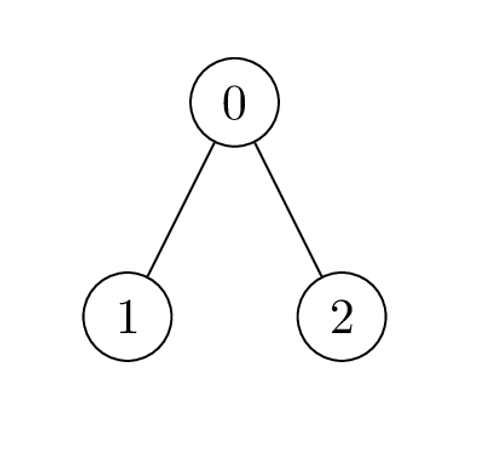
Input: edges = [[0,1],[0,2]], cost = [1,2,-2] Output: [0,1,1] Explanation: Node 1 and 2 are leaves with subtree of size 1, place 1 coin on each of them. For node 0 the only possible product of cost is 2 * 1 * -2 = -4. Hence place 0 coins on node 0.
Constraints:
2 <= n <= 2 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < ncost.length == n1 <= |cost[i]| <= 104- The input is generated such that
edgesrepresents a valid tree.
Solution
Python3
class Solution:
def placedCoins(self, edges: List[List[int]], cost: List[int]) -> List[int]:
n = len(cost)
graph = defaultdict(list)
res = [0] * n
for x, y in edges:
graph[x].append(y)
graph[y].append(x)
def go(node, prev):
nonlocal res
big = [cost[node]]
small = [cost[node]]
for adj in graph[node]:
if adj != prev:
b, s = go(adj, node)
big += b
small += s
big = sorted(big, reverse = 1)[:3]
small = sorted(small)[:2]
if len(big) < 3:
res[node] = 1
else:
res[node] = max(0, big[0] * big[1] * big[2], big[0] * small[0] * small[1])
return big, small
go(0, -1)
return res