1631. Path With Minimum Effort

Problem Link

Description

---

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

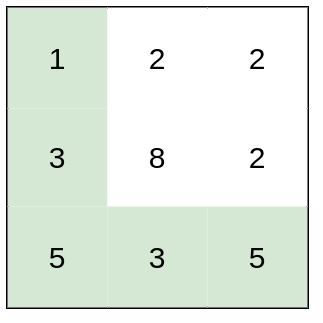
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

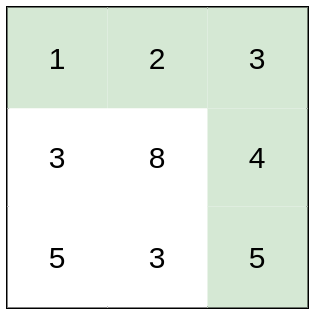
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

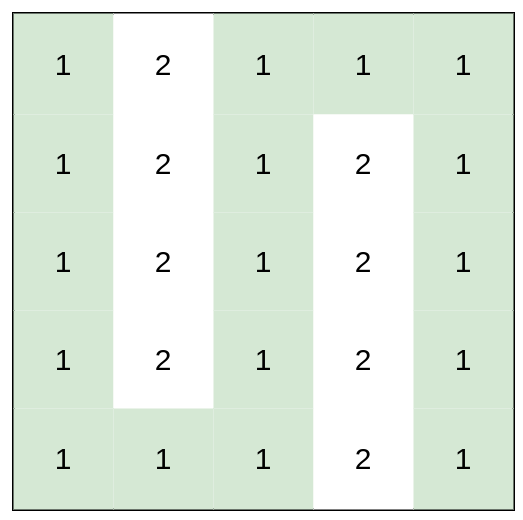
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

Solution

---

Python3

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        rows, cols = len(heights), len(heights[0])
        dist = [[inf] * cols for _ in range(rows)]
        dist[0][0] = 0
        pq = [(0, 0, 0)]
 
        while pq:
            d, x, y = heappop(pq)
 
            if dist[x][y] != d: continue
 
            if x == rows - 1 and y == cols - 1: return d
 
            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols:
                    oldDist = dist[dx][dy]
                    newDist = max(d, abs(heights[dx][dy] - heights[x][y]))
 
                    if newDist < oldDist:
                        dist[dx][dy] = newDist
                        heappush(pq, (newDist, dx, dy))
        
        return -1