3547. Maximum Sum of Edge Values in a Graph

Problem Link

Description

---

You are given an undirected connected graph of n nodes, numbered from 0 to n - 1. Each node is connected to at most 2 other nodes.

The graph consists of m edges, represented by a 2D array edges, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi.

You have to assign a unique value from 1 to n to each node. The value of an edge will be the product of the values assigned to the two nodes it connects.

Your score is the sum of the values of all edges in the graph.

Return the maximum score you can achieve.

 

Example 1:

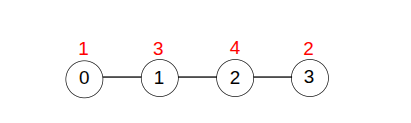
Input: n = 4, edges = [[0,1],[1,2],[2,3]]

Output: 23

Explanation:

The diagram above illustrates an optimal assignment of values to nodes. The sum of the values of the edges is: (1 * 3) + (3 * 4) + (4 * 2) = 23.

Example 2:

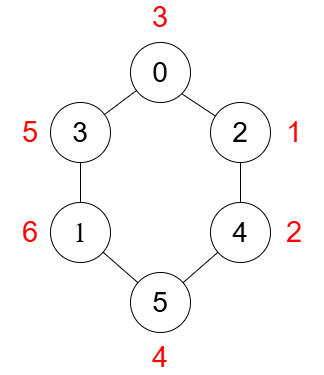
Input: n = 6, edges = [[0,3],[4,5],[2,0],[1,3],[2,4],[1,5]]

Output: 82

Explanation:

The diagram above illustrates an optimal assignment of values to nodes. The sum of the values of the edges is: (1 * 2) + (2 * 4) + (4 * 6) + (6 * 5) + (5 * 3) + (3 * 1) = 82.

 

Constraints:

• 1 <= n <= 5 * 104
• m == edges.length
• 1 <= m <= n
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.
• The graph is connected.
• Each node is connected to at most 2 other nodes.

Solution

---

Python3

class Solution:
    def maxScore(self, n: int, edges: List[List[int]]) -> int:
        graph = defaultdict(list)
 
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
 
        def getComp(node):
            bfs = [node]
            visited[node] = True
            for node in bfs:
                for adj in graph[node]:
                    if not visited[adj]:
                        visited[adj] = True
                        bfs.append(adj)
            return bfs
 
        visited = [False] * n
        cycles = []
        paths = []
        for node in range(n):
            if visited[node]: continue
 
            comp = getComp(node)
            if all(len(graph[x]) == 2 for x in comp):
                cycles.append(len(comp))
            elif len(comp) > 1:
                paths.append(len(comp))
        
        def calc(left, right, isCycle):
            res = 0
            q = deque([right, right])
 
            for a in range(right - 1, left - 1, -1):
                v = q.popleft()
                res += a * v
                q.append(a)
            
            return res + q[0] * q[1] * isCycle
        
        res = 0
 
        for length in cycles:
            res += calc(n - length + 1, n, 1)
            n -= length
 
        paths.sort(reverse = 1)
        for length in paths:
            res += calc(n - length + 1, n, 0)
            n -= length
    
        return res