3249. Count the Number of Good Nodes

Problem Link

Description

---

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

A node is good if all the subtrees rooted at its children have the same size.

Return the number of good nodes in the given tree.

A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.

 

Example 1:

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

Output: 7

Explanation:

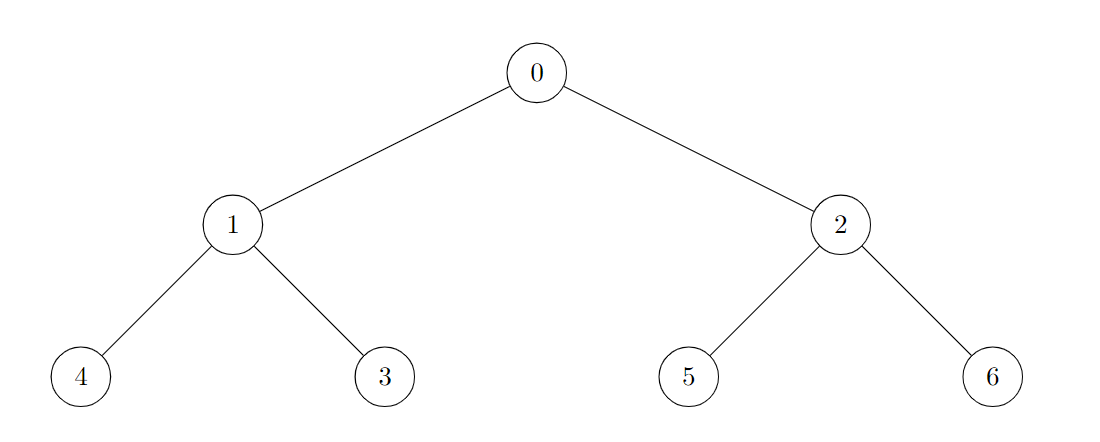
All of the nodes of the given tree are good.

Example 2:

Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

Output: 6

Explanation:

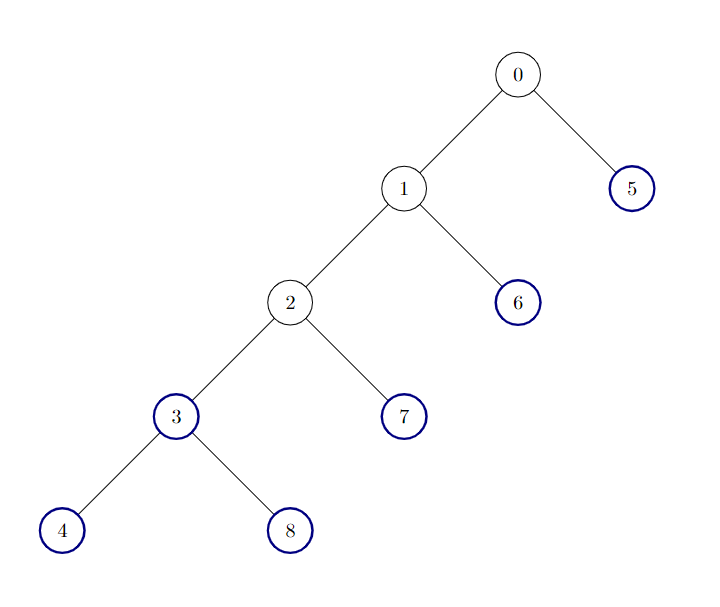
There are 6 good nodes in the given tree. They are colored in the image above.

Example 3:

Input: edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

Output: 12

Explanation:

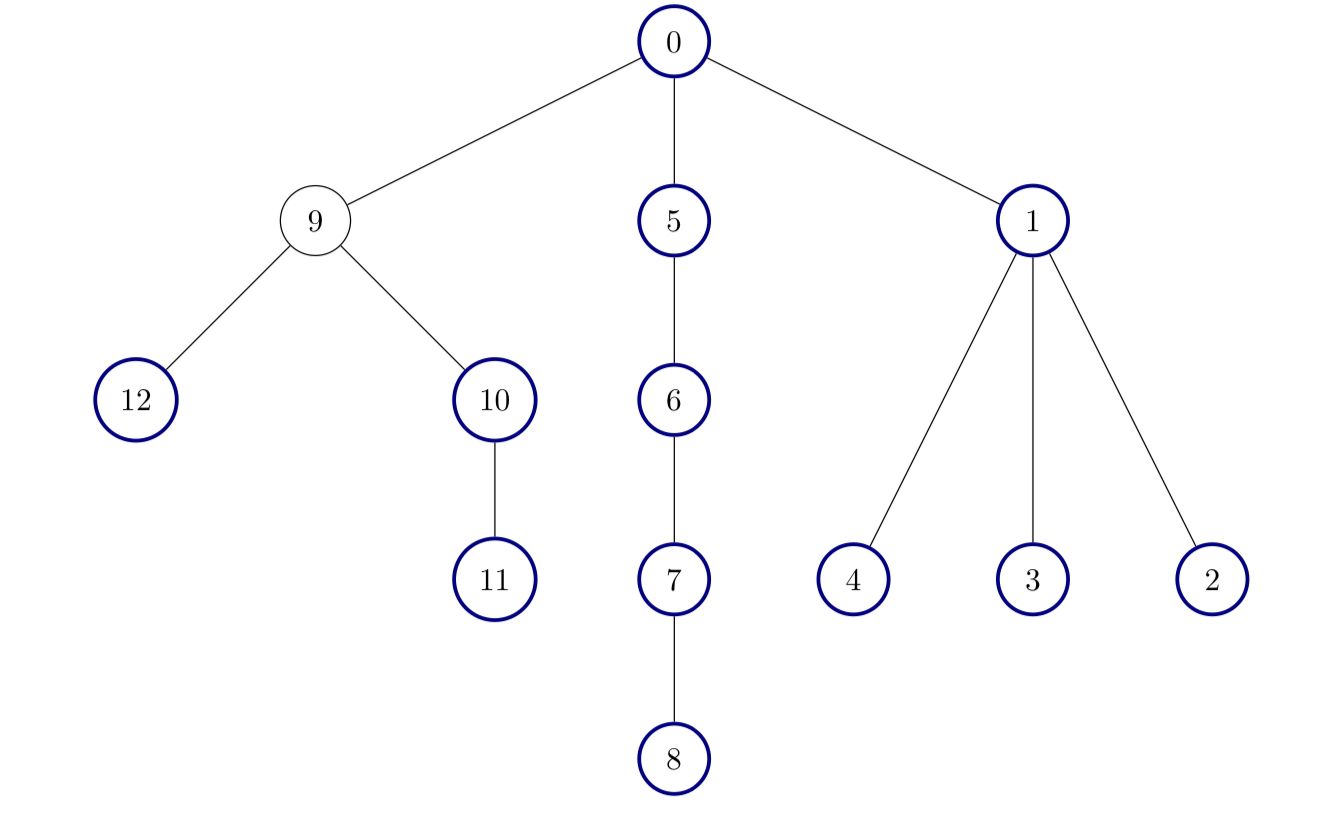
All nodes except node 9 are good.

 

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• The input is generated such that edges represents a valid tree.

Solution

---

Python3

class Solution:
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        N = len(edges) + 1
        graph = defaultdict(list)
        res = 0
        sz = [0] * N
 
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        
        def go(node, prev):
            count = 1
 
            for adj in graph[node]:
                if adj != prev:
                    count += go(adj, node)
            
            sz[node] = count
 
            return count
        
        go(0, -1)
 
        for node in range(N):
            ok = True
            prev = -1
 
            for adj in graph[node]:
                if sz[adj] < sz[node]:
                    if prev == -1:
                        prev = sz[adj]
                    elif prev != sz[adj]:
                        ok = False
                        break
 
            if ok: res += 1
        
        return res