2385. Amount of Time for Binary Tree to Be Infected

Problem Link

Description

---

You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

• The node is currently uninfected.
• The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

 

Example 1:

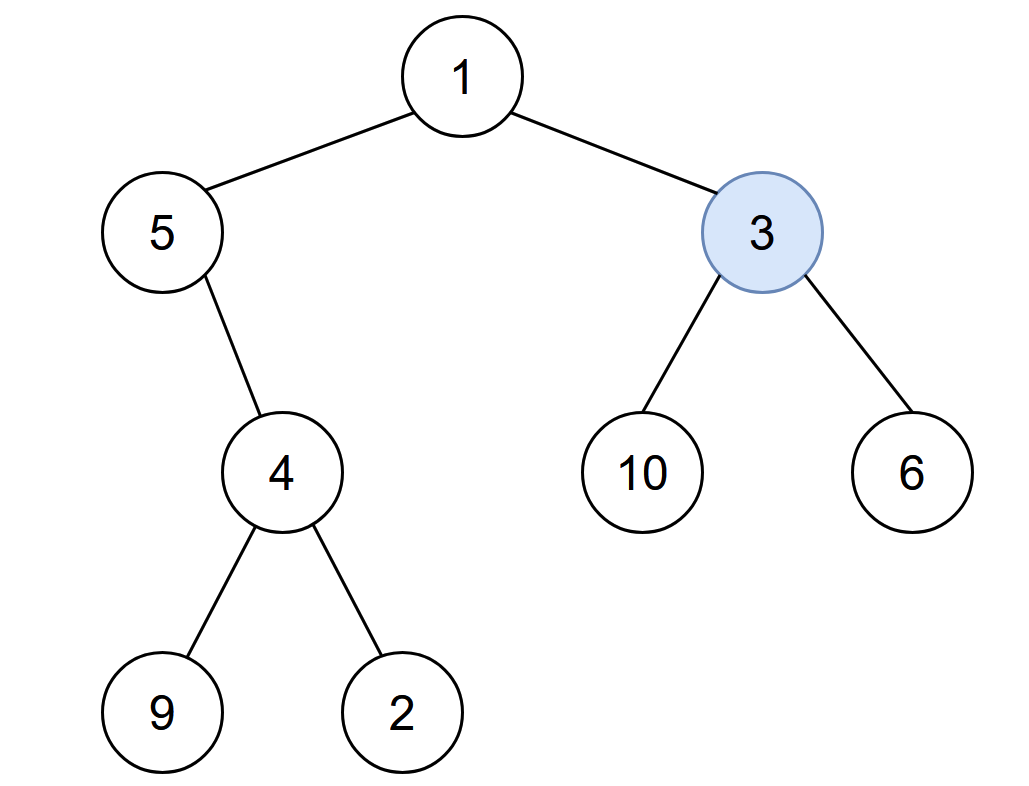
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 105
• Each node has a unique value.
• A node with a value of start exists in the tree.

Solution

---

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        graph = defaultdict(list)
 
        def go(node, prev):
            if not node: return
 
            if prev:
                graph[prev.val].append(node.val)
                graph[node.val].append(prev.val)
            
            go(node.left, node)
            go(node.right, node)
 
        go(root, None)
        
        queue = deque([start])
        visited = set()
        visited.add(start)
        time = -1
 
        while queue:
            for _ in range(len(queue)):
                node = queue.popleft()
                for adj in graph[node]:
                    if adj not in visited:
                        visited.add(adj)
                        queue.append(adj)
            
            time += 1
        
        return time