329. Longest Increasing Path in a Matrix

Problem Link

Description

---

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

 

Example 1:

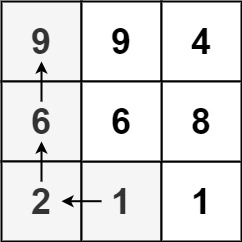
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

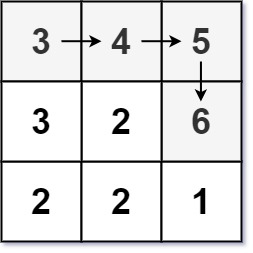
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = [[1]]
Output: 1

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

Solution

---

Python3

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        rows, cols = len(matrix), len(matrix[0])
        
        @cache
        def go(x, y):
            count = 1
            
            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and matrix[dx][dy] > matrix[x][y]:
                    count = max(count, 1 + go(dx, dy))
            
            return count
        
        res = 0
        
        for x in range(rows):
            for y in range(cols):
                res = max(res, go(x, y))
        
        return res