979. Distribute Coins in Binary Tree

Problem Link

Description

---

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

 

Example 1:

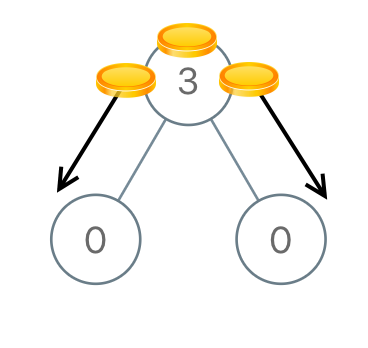
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

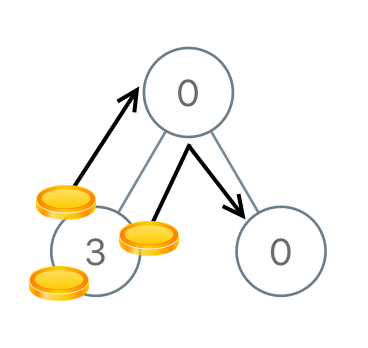
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

 

Constraints:

• The number of nodes in the tree is n.
• 1 <= n <= 100
• 0 <= Node.val <= n
• The sum of all Node.val is n.

Solution

---

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def distributeCoins(self, root: Optional[TreeNode]) -> int:
        res = 0
        
        def go(node):
            nonlocal res
 
            if not node: return 0
 
            left, right = go(node.left), go(node.right)
            coins = left + right + node.val
            res += abs(coins - 1)
 
            return coins - 1
        
        go(root)
        return res