3242. Design Neighbor Sum Service

Problem Link

Description

---

You are given a n x n 2D array grid containing distinct elements in the range [0, n2 - 1].

Implement the NeighborSum class:

• NeighborSum(int [][]grid) initializes the object.
• int adjacentSum(int value) returns the sum of elements which are adjacent neighbors of value, that is either to the top, left, right, or bottom of value in grid.
• int diagonalSum(int value) returns the sum of elements which are diagonal neighbors of value, that is either to the top-left, top-right, bottom-left, or bottom-right of value in grid.

 

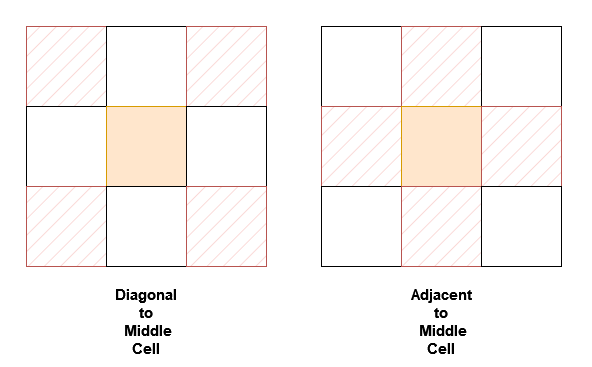
Example 1:

Input:

["NeighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

Output: [null, 6, 16, 16, 4]

Explanation:

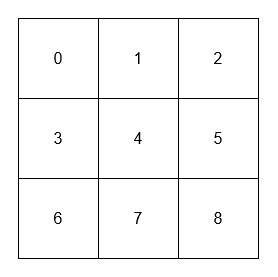
• The adjacent neighbors of 1 are 0, 2, and 4.
• The adjacent neighbors of 4 are 1, 3, 5, and 7.
• The diagonal neighbors of 4 are 0, 2, 6, and 8.
• The diagonal neighbor of 8 is 4.

Example 2:

Input:

["NeighborSum", "adjacentSum", "diagonalSum"]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

Output: [null, 23, 45]

Explanation:

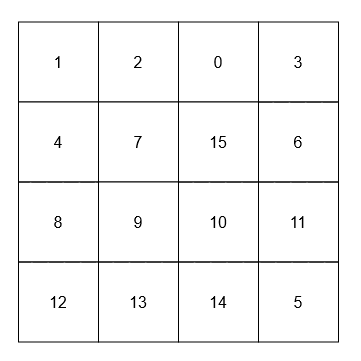
• The adjacent neighbors of 15 are 0, 10, 7, and 6.
• The diagonal neighbors of 9 are 4, 12, 14, and 15.

 

Constraints:

• 3 <= n == grid.length == grid[0].length <= 10
• 0 <= grid[i][j] <= n2 - 1
• All grid[i][j] are distinct.
• value in adjacentSum and diagonalSum will be in the range [0, n2 - 1].
• At most 2 * n2 calls will be made to adjacentSum and diagonalSum.

Solution

---

Python3

class neighborSum:
 
    def __init__(self, grid: List[List[int]]):
        self.grid = grid
        self.rows = len(grid)
        self.cols = len(grid[0])
        self.pos = {}
 
        for i in range(self.rows):
            for j in range(self.cols):
                self.pos[grid[i][j]] = (i, j)
 
    def adjacentSum(self, value: int) -> int:
        i, j = self.pos[value]
        res = 0
 
        for dx, dy in [(i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1)]:
            if 0 <= dx < self.rows and 0 <= dy < self.cols:
                res += self.grid[dx][dy]
        
        return res
 
    def diagonalSum(self, value: int) -> int:
        i, j = self.pos[value]
        res = 0
 
        for dx, dy in [(i - 1, j - 1), (i - 1, j + 1), (i + 1, j + 1), (i + 1, j - 1)]:
            if 0 <= dx < self.rows and 0 <= dy < self.cols:
                res += self.grid[dx][dy]
        
        return res
 
 
# Your neighborSum object will be instantiated and called as such:
# obj = neighborSum(grid)
# param_1 = obj.adjacentSum(value)
# param_2 = obj.diagonalSum(value)