1235. Maximum Profit in Job Scheduling

Problem Link

Description

---

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

 

Example 1:

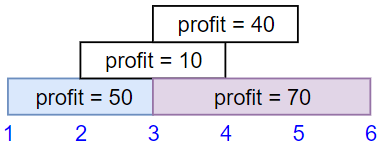
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

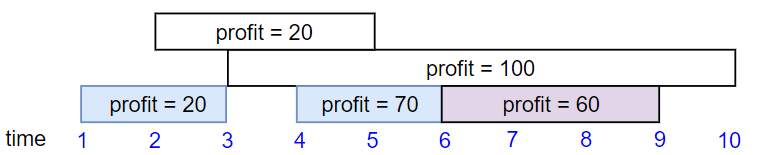
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

 

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 104
• 1 <= startTime[i] < endTime[i] <= 109
• 1 <= profit[i] <= 104

Solution

---

Python3

class Solution:
    def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
        N = len(startTime)
        A = sorted([[s, e, p] for s, e, p in zip(startTime, endTime, profit)], key = lambda x : (x[0]))
 
        @cache
        def go(index):
            if index == N: return 0
 
            # skip
            res = go(index + 1)
 
            # take
            end = A[index][1]
            j = bisect_left(A, end, key = lambda x : x[0])
            res = max(res, A[index][2] + go(j))
 
            return res
 
        return go(0)