3044. Most Frequent Prime

Problem Link

Description

---

You are given a m x n 0-indexed 2D matrix mat. From every cell, you can create numbers in the following way:

• There could be at most 8 paths from the cells namely: east, south-east, south, south-west, west, north-west, north, and north-east.
• Select a path from them and append digits in this path to the number being formed by traveling in this direction.
• Note that numbers are generated at every step, for example, if the digits along the path are 1, 9, 1, then there will be three numbers generated along the way: 1, 19, 191.

Return the most frequent prime number greater than 10 out of all the numbers created by traversing the matrix or -1 if no such prime number exists. If there are multiple prime numbers with the highest frequency, then return the largest among them.

Note: It is invalid to change the direction during the move.

 

Example 1:

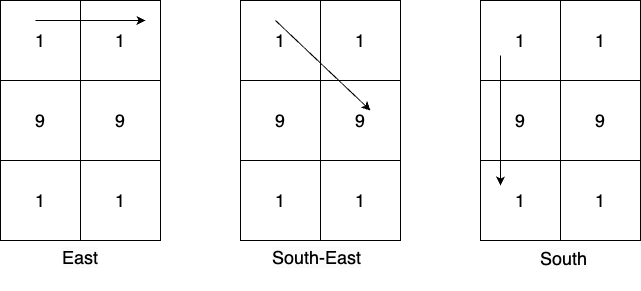
Input: mat = [[1,1],[9,9],[1,1]]
Output: 19
Explanation: 
From cell (0,0) there are 3 possible directions and the numbers greater than 10 which can be created in those directions are:
East: [11], South-East: [19], South: [19,191].
Numbers greater than 10 created from the cell (0,1) in all possible directions are: [19,191,19,11].
Numbers greater than 10 created from the cell (1,0) in all possible directions are: [99,91,91,91,91].
Numbers greater than 10 created from the cell (1,1) in all possible directions are: [91,91,99,91,91].
Numbers greater than 10 created from the cell (2,0) in all possible directions are: [11,19,191,19].
Numbers greater than 10 created from the cell (2,1) in all possible directions are: [11,19,19,191].
The most frequent prime number among all the created numbers is 19.

Example 2:

Input: mat = [[7]]
Output: -1
Explanation: The only number which can be formed is 7. It is a prime number however it is not greater than 10, so return -1.

Example 3:

Input: mat = [[9,7,8],[4,6,5],[2,8,6]]
Output: 97
Explanation: 
Numbers greater than 10 created from the cell (0,0) in all possible directions are: [97,978,96,966,94,942].
Numbers greater than 10 created from the cell (0,1) in all possible directions are: [78,75,76,768,74,79].
Numbers greater than 10 created from the cell (0,2) in all possible directions are: [85,856,86,862,87,879].
Numbers greater than 10 created from the cell (1,0) in all possible directions are: [46,465,48,42,49,47].
Numbers greater than 10 created from the cell (1,1) in all possible directions are: [65,66,68,62,64,69,67,68].
Numbers greater than 10 created from the cell (1,2) in all possible directions are: [56,58,56,564,57,58].
Numbers greater than 10 created from the cell (2,0) in all possible directions are: [28,286,24,249,26,268].
Numbers greater than 10 created from the cell (2,1) in all possible directions are: [86,82,84,86,867,85].
Numbers greater than 10 created from the cell (2,2) in all possible directions are: [68,682,66,669,65,658].
The most frequent prime number among all the created numbers is 97.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 6
• 1 <= mat[i][j] <= 9

Solution

---

Python3

def sieve(limit):
    is_prime = [True] * (limit + 1)
    is_prime[0] = is_prime[1] = False
 
    for number in range(2, limit + 1):
        if is_prime[number]:
            for multiple in range(number * number, limit + 1, number):
                is_prime[multiple] = False
 
    return is_prime
 
PRIMES = sieve(10 ** 7)
 
class Solution:
    def mostFrequentPrime(self, mat: List[List[int]]) -> int:
        rows, cols = len(mat), len(mat[0])
        counter = Counter()
 
        for i in range(rows):
            for j in range(cols):
                for di in range(-1, 2):
                    for dj in range(-1, 2):
                        if di == dj == 0: continue
                        
                        num = 0
                        
                        ci, cj = i, j
 
                        while 0 <= ci < rows and 0 <= cj < cols:
                            num = num * 10 + mat[ci][cj]
                            ci += di
                            cj += dj
                        
                            if num > 10 and PRIMES[num]:
                                counter[num] += 1
 
        if len(counter) == 0: return -1
        
        maxFreq = max(counter.values())
        res = -1
        
        for k, v in counter.items():
            if v == maxFreq:
                res = max(res, k)
        
        return res