684. Redundant Connection

Problem Link

Description

---

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

Example 1:

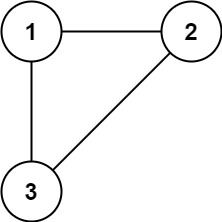
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

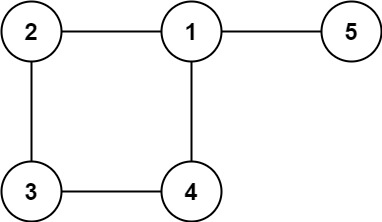
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Solution

---

Python3

class DSU:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.rank = [0 for _ in range(n)]
 
    def find(self, x):
        if self.parent[x] == x:
            return self.parent[x]
        self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
 
    def union(self, u, v, pu, pv):
        # pu = self.find(u)
        # pv = self.find(v)
 
        if (pu == pv): return
 
        if self.rank[pu] < self.rank[pv]:
            pu, pv = pv, pu
 
        # ensure self.rank[pu] >= self.rank[pv]
        self.parent[pv] = pu
        if self.rank[pu] == self.rank[pv]:
            self.rank[pu] += 1
 
class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        N = len(edges)
        uf = DSU(N + 1)
 
        for a, b in edges:
            pa, pb = uf.find(a), uf.find(b)
 
            if pa == pb:
                return [a, b]
            else:
                uf.union(a, b, pa, pb)
        
        return []