3575. Maximum Good Subtree Score

Problem Link

Description

---

You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1. Each node i has an integer value vals[i], and its parent is given by par[i].

A subset of nodes within the subtree of a node is called good if every digit from 0 to 9 appears at most once in the decimal representation of the values of the selected nodes.

The score of a good subset is the sum of the values of its nodes.

Define an array maxScore of length n, where maxScore[u] represents the maximum possible sum of values of a good subset of nodes that belong to the subtree rooted at node u, including u itself and all its descendants.

Return the sum of all values in maxScore.

Since the answer may be large, return it modulo 109 + 7.

 

Example 1:

Input: vals = [2,3], par = [-1,0]

Output: 8

Explanation:

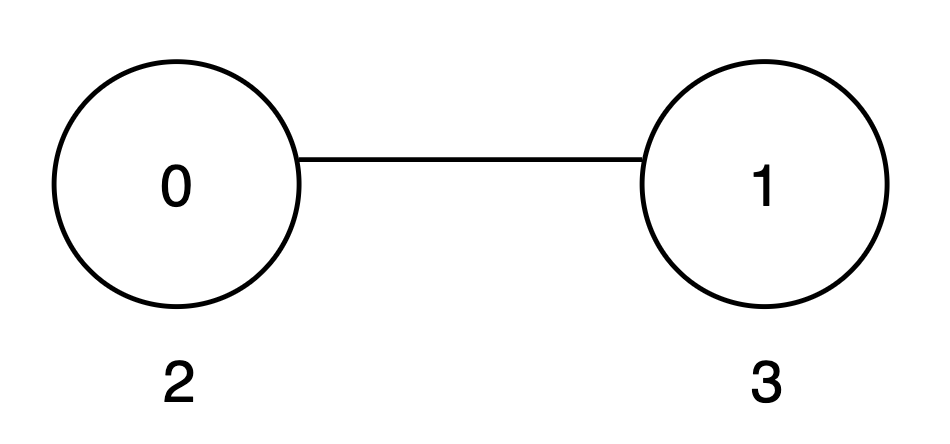
• The subtree rooted at node 0 includes nodes {0, 1}. The subset {2, 3} is good as the digits 2 and 3 appear only once. The score of this subset is 2 + 3 = 5.
• The subtree rooted at node 1 includes only node {1}. The subset {3} is good. The score of this subset is 3.
• The maxScore array is [5, 3], and the sum of all values in maxScore is 5 + 3 = 8. Thus, the answer is 8.

Example 2:

Input: vals = [1,5,2], par = [-1,0,0]

Output: 15

Explanation:

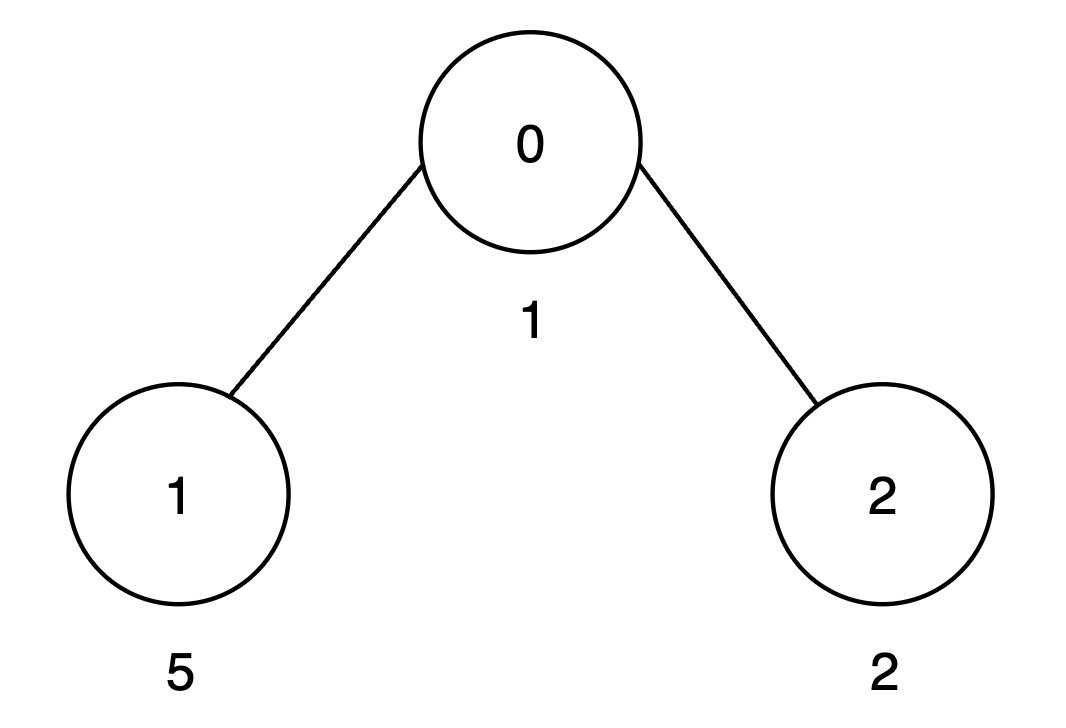
• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {1, 5, 2} is good as the digits 1, 5 and 2 appear only once. The score of this subset is 1 + 5 + 2 = 8.
• The subtree rooted at node 1 includes only node {1}. The subset {5} is good. The score of this subset is 5.
• The subtree rooted at node 2 includes only node {2}. The subset {2} is good. The score of this subset is 2.
• The maxScore array is [8, 5, 2], and the sum of all values in maxScore is 8 + 5 + 2 = 15. Thus, the answer is 15.

Example 3:

Input: vals = [34,1,2], par = [-1,0,1]

Output: 42

Explanation:

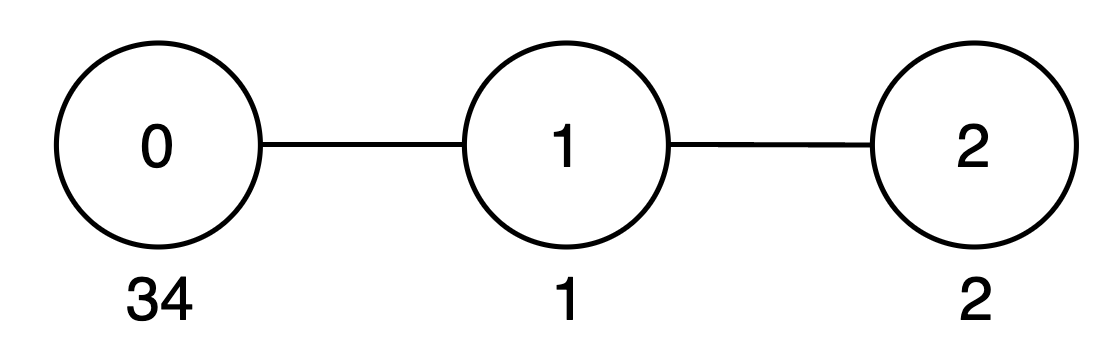
• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {34, 1, 2} is good as the digits 3, 4, 1 and 2 appear only once. The score of this subset is 34 + 1 + 2 = 37.
• The subtree rooted at node 1 includes node {1, 2}. The subset {1, 2} is good as the digits 1 and 2 appear only once. The score of this subset is 1 + 2 = 3.
• The subtree rooted at node 2 includes only node {2}. The subset {2} is good. The score of this subset is 2.
• The maxScore array is [37, 3, 2], and the sum of all values in maxScore is 37 + 3 + 2 = 42. Thus, the answer is 42.

Example 4:

Input: vals = [3,22,5], par = [-1,0,1]

Output: 18

Explanation:

• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {3, 22, 5} is not good, as digit 2 appears twice. Therefore, the subset {3, 5} is valid. The score of this subset is 3 + 5 = 8.
• The subtree rooted at node 1 includes nodes {1, 2}. The subset {22, 5} is not good, as digit 2 appears twice. Therefore, the subset {5} is valid. The score of this subset is 5.
• The subtree rooted at node 2 includes {2}. The subset {5} is good. The score of this subset is 5.
• The maxScore array is [8, 5, 5], and the sum of all values in maxScore is 8 + 5 + 5 = 18. Thus, the answer is 18.

 

Constraints:

• 1 <= n == vals.length <= 500
• 1 <= vals[i] <= 109
• par.length == n
• par[0] == -1
• 0 <= par[i] < n for i in [1, n - 1]
• The input is generated such that the parent array par represents a valid tree.

Solution

---

Python3

class Solution:
    def goodSubtreeSum(self, vals: List[int], par: List[int]) -> int:
        N = len(vals)
        M = 10 ** 9 + 7
        graph = defaultdict(list)
        ans = 0
 
        for node, p in enumerate(par):
            if p != -1:
                graph[p].append(node)
 
        def isDup(d, mask):
            newMask = mask
 
            while d > 0:
                rem = d % 10
                if newMask & (1 << rem) == 0:
                    newMask |= (1 << rem)
                else:
                    return True, mask
 
                d //= 10
            
            return False, newMask
 
        def helper(node):
            nonlocal ans
            A = [vals[node]]
 
            for adj in graph[node]:
                child = helper(adj)
                A.extend(child)
            
            @cache
            def dp(index, mask):
                if index == len(A): return 0
 
                # skip
                curr = dp(index + 1, mask)
 
                # take if it's valid
                isDuplicate, newMask = isDup(A[index], mask)
                if not isDuplicate:
                    curr = max(curr, A[index] + dp(index + 1, newMask))
 
                return curr
 
 
            res = dp(0, 0)
            ans += res
            ans %= M
 
            return A
 
        helper(0)
        return ans