2791. Count Paths That Can Form a Palindrome in a Tree

Problem Link

Description

---

You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to n - 1. The tree is represented by a 0-indexed array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to the edge between i and parent[i]. s[0] can be ignored.

Return the number of pairs of nodes (u, v) such that u < v and the characters assigned to edges on the path from u to v can be rearranged to form a palindrome.

A string is a palindrome when it reads the same backwards as forwards.

 

Example 1:

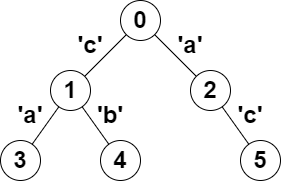
Input: parent = [-1,0,0,1,1,2], s = "acaabc"
Output: 8
Explanation: The valid pairs are:
- All the pairs (0,1), (0,2), (1,3), (1,4) and (2,5) result in one character which is always a palindrome.
- The pair (2,3) result in the string "aca" which is a palindrome.
- The pair (1,5) result in the string "cac" which is a palindrome.
- The pair (3,5) result in the string "acac" which can be rearranged into the palindrome "acca".

Example 2:

Input: parent = [-1,0,0,0,0], s = "aaaaa"
Output: 10
Explanation: Any pair of nodes (u,v) where u < v is valid.

 

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1
• parent[0] == -1
• parent represents a valid tree.
• s consists of only lowercase English letters.

Solution

---

Python3

class Solution:
    def countPalindromePaths(self, parent: List[int], s: str) -> int:
        N = len(parent)
 
        @cache
        def f(node):
            return f(parent[node]) ^ (1 << (ord(s[node]) - ord('a'))) if node else 0
        
        res = 0
        mp = Counter()
 
        for node in range(N):
            v = f(node)
 
            res += mp[v] + sum(mp[v ^ (1 << k)] for k in range(26))
            
            mp[v] += 1
 
        return res
 

C++

class Solution {
public:
    long long countPalindromePaths(vector<int>& parent, string s) {
        int N = parent.size();
        vector<long long> mp(N);
        unordered_map<long long, long long> counter;
        vector<vector<int>> graph(N, vector<int>());
 
        for (int node = 0; node < N; node++) {
            if (parent[node] != -1) 
                graph[parent[node]].push_back(node);
        }
        
        function<void(int, long long)> dfs = [&](int node, long long mask) {
            mp[node] = mask;
            
            for (int adj: graph[node])
                dfs(adj, mask ^ (1LL << (s[adj] - 'a')));   
        };
        
        dfs(0, 0);
        
        long long res = 0;
        for (int node = 0; node < N; node++) {
            long long mask = mp[node];
            
            res += counter[mask];
            
            for (int mid = 0; mid < 26; mid++) {
                res += counter[mask ^ (1LL << mid)];
            }
            
            counter[mask]++;
        }
        
        return res;
    }
};