2617. Minimum Number of Visited Cells in a Grid

Problem Link

Description

---

You are given a 0-indexed m x n integer matrix grid. Your initial position is at the top-left cell (0, 0).

Starting from the cell (i, j), you can move to one of the following cells:

• Cells (i, k) with j < k <= grid[i][j] + j (rightward movement), or
• Cells (k, j) with i < k <= grid[i][j] + i (downward movement).

Return the minimum number of cells you need to visit to reach the bottom-right cell (m - 1, n - 1). If there is no valid path, return -1.

 

Example 1:

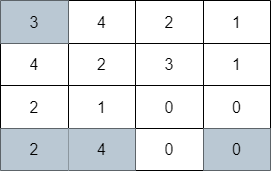
Input: grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
Output: 4
Explanation: The image above shows one of the paths that visits exactly 4 cells.

Example 2:

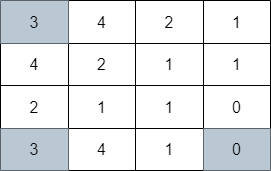
Input: grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
Output: 3
Explanation: The image above shows one of the paths that visits exactly 3 cells.

Example 3:

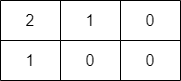
Input: grid = [[2,1,0],[1,0,0]]
Output: -1
Explanation: It can be proven that no path exists.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= grid[i][j] < m * n
• grid[m - 1][n - 1] == 0

Solution

---

Python3

from sortedcontainers import SortedList
 
class Solution:
    def minimumVisitedCells(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
        R = [SortedList(range(cols)) for _ in range(rows)]
        C = [SortedList(range(rows)) for _ in range(cols)]
        pq = [(1, 0, 0)]
        
        while pq:
            d, r, c = heappop(pq)
            
            if (r, c) == (rows - 1, cols - 1):
                return d
            
            index = R[r].bisect_left(c + 1)
            while index < len(R[r]) and R[r][index] <= grid[r][c] + c:
                nr, nc = r, R[r][index]
                heappush(pq, (d + 1, nr, nc))
                
                R[nr].remove(nc)
                C[nc].remove(nr)
            
            index = C[c].bisect_left(r + 1)
            while index < len(C[c]) and C[c][index] <= grid[r][c] + r:
                nr, nc = C[c][index], c
                heappush(pq, (d + 1, nr, nc))
                
                R[nr].remove(nc)
                C[nc].remove(nr)
        
        return -1