802. Find Eventual Safe States

Problem Link

Description

---

There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].

A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).

Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.

 

Example 1:

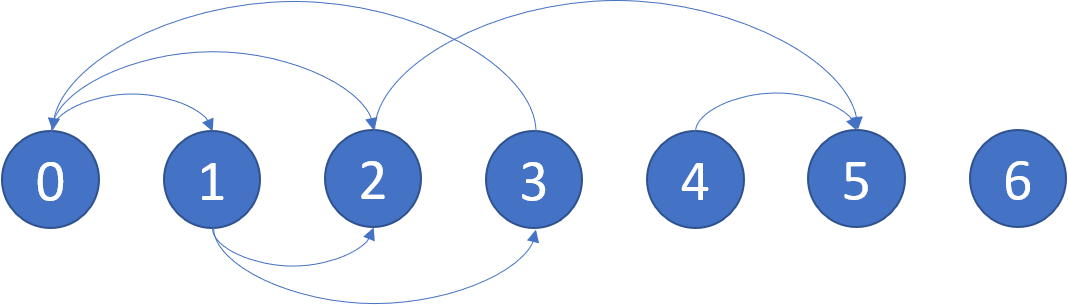
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Example 2:

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

 

Constraints:

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].length <= n
• 0 <= graph[i][j] <= n - 1
• graph[i] is sorted in a strictly increasing order.
• The graph may contain self-loops.
• The number of edges in the graph will be in the range [1, 4 * 104].

Solution

---

Python3

class Solution:
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        N = len(graph)
        G = defaultdict(list) # reverse graph
        outdegree = [len(edges) for edges in graph]
        queue = deque()
        res = []
 
        for node in range(N):
            for edge in graph[node]:
                G[edge].append(node)
            
            if outdegree[node] == 0:
                queue.append(node)
                res.append(node)
 
        while queue:
            node = queue.popleft()
 
            for adj in G[node]:
                outdegree[adj] -= 1
 
                if outdegree[adj] == 0:
                    res.append(adj)
                    queue.append(adj)
 
        return sorted(res)