1335. Minimum Difficulty of a Job Schedule

Problem Link

Description

---

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

 

Example 1:

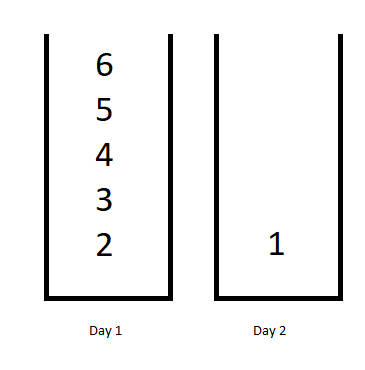
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7 

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

 

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

Solution

---

Python3

class Solution:
    def minDifficulty(self, jobs: List[int], d: int) -> int:
        N = len(jobs)
        if N < d: return -1
 
        @cache
        def go(index, d):
            if d < 0: return inf
 
            if index == N:
                return 0 if d == 0 else inf
            
            res = jobs[index] + go(index + 1, d - 1)
 
            curr = jobs[index]
            for j in range(index + 1, N):
                curr = max(curr, jobs[j])
 
                res = min(res, curr + go(j + 1, d - 1))
            
            return res
        
        return go(0, d)