3544. Subtree Inversion Sum

Problem Link

Description

---

You are given an undirected tree rooted at node 0, with n nodes numbered from 0 to n - 1. The tree is represented by a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates an edge between nodes ui and vi.

You are also given an integer array nums of length n, where nums[i] represents the value at node i, and an integer k.

You may perform inversion operations on a subset of nodes subject to the following rules:

• Subtree Inversion Operation:

  <ul data-end="890" data-start="802">
  	<li data-end="887" data-start="802">
  	<p data-end="887" data-start="804">When you invert a node, every value in the <span data-keyword="subtree-of-node">subtree</span> rooted at that node is multiplied by -1.</p>
  	</li>
  </ul>
  </li>
  <li data-end="1247" data-start="891">
  <p data-end="931" data-start="893"><strong data-end="931" data-start="893">Distance Constraint on Inversions:</strong></p>
  
  <ul data-end="1247" data-start="934">
  	<li data-end="1020" data-start="934">
  	<p data-end="1020" data-start="936">You may only invert a node if it is &quot;sufficiently far&quot; from any other inverted node.</p>
  	</li>
  	<li data-end="1247" data-start="1023">
  	<p data-end="1247" data-start="1025">Specifically, if you invert two nodes <code>a</code> and <code>b</code> such that one is an ancestor of the other (i.e., if <code>LCA(a, b) = a</code> or <code>LCA(a, b) = b</code>), then the distance (the number of edges on the unique path between them) must be at least <code>k</code>.</p>
  	</li>
  </ul>
  </li>
  

Return the maximum possible sum of the tree's node values after applying inversion operations.

 

Example 1:

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], nums = [4,-8,-6,3,7,-2,5], k = 2

Output: 27

Explanation:

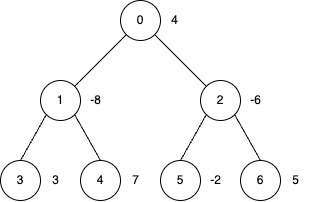
• Apply inversion operations at nodes 0, 3, 4 and 6.
• The final nums array is [-4, 8, 6, 3, 7, 2, 5], and the total sum is 27.

Example 2:

Input: edges = [[0,1],[1,2],[2,3],[3,4]], nums = [-1,3,-2,4,-5], k = 2

Output: 9

Explanation:

• Apply the inversion operation at node 4.
• The final nums array becomes [-1, 3, -2, 4, 5], and the total sum is 9.

Example 3:

Input: edges = [[0,1],[0,2]], nums = [0,-1,-2], k = 3

Output: 3

Explanation:

Apply inversion operations at nodes 1 and 2.

 

Constraints:

• 2 <= n <= 5 * 104
• edges.length == n - 1
• edges[i] = [ui, vi]
• 0 <= ui, vi < n
• nums.length == n
• -5 * 104 <= nums[i] <= 5 * 104
• 1 <= k <= 50
• The input is generated such that edges represents a valid tree.

Solution

---

Python3

class Solution:
    def subtreeInversionSum(self, edges: List[List[int]], nums: List[int], k: int) -> int:
        N = len(edges) + 1
        graph = defaultdict(list)
 
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)
        
        parent = [-1] * N
 
        @cache
        def dfs(node, flip, since_last):
            curr = -nums[node] if flip else nums[node]
            if_flip = -curr
 
            for adj in graph[node]:
                if adj != parent[node]:
                    parent[adj] = node
                    curr += dfs(adj, flip, min(since_last + 1, k))
                
                    if since_last == k:
                        if_flip += dfs(adj, not flip, 1)
            
            if since_last == k:
                return max(curr, if_flip)
            
            return curr
        
        return dfs(0, False, k)