2641. Cousins in Binary Tree II

Problem Link

Description

---

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

 

Example 1:

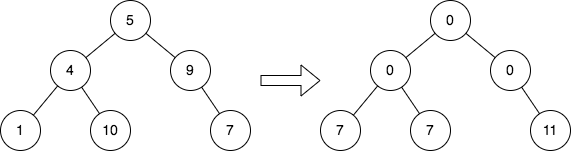
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 104

Solution

---

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def replaceValueInTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # total[level] = sum
        total = defaultdict(int)
        # parents[parent] = sum
        parents = defaultdict(int)
        
        def dfs1(node, level, parent):
            if not node: return
 
            parents[parent] += node.val
            total[level] += node.val
 
            dfs1(node.left, level + 1, node)
            dfs1(node.right, level + 1, node)
        
        dfs1(root, 0, -1)
 
        def dfs2(node, level, parent):
            if not node: return None
 
            node.left = dfs2(node.left, level + 1, node)
            node.right = dfs2(node.right, level + 1, node)
 
            node.val = total[level] - parents[parent]
 
            return node
        
        return dfs2(root, 0, -1)