3531. Count Covered Buildings

Problem Link

Description

---

You are given a positive integer n, representing an n x n city. You are also given a 2D grid buildings, where buildings[i] = [x, y] denotes a unique building located at coordinates [x, y].

A building is covered if there is at least one building in all four directions: left, right, above, and below.

Return the number of covered buildings.

 

Example 1:

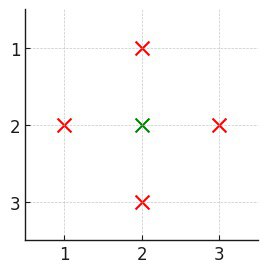
Input: n = 3, buildings = [[1,2],[2,2],[3,2],[2,1],[2,3]]

Output: 1

Explanation:

• Only building [2,2] is covered as it has at least one building:

  <ul>
  	<li>above (<code>[1,2]</code>)</li>
  	<li>below (<code>[3,2]</code>)</li>
  	<li>left (<code>[2,1]</code>)</li>
  	<li>right (<code>[2,3]</code>)</li>
  </ul>
  </li>
  <li>Thus, the count of covered buildings is 1.</li>
  

Example 2:

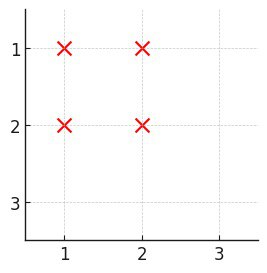
Input: n = 3, buildings = [[1,1],[1,2],[2,1],[2,2]]

Output: 0

Explanation:

• No building has at least one building in all four directions.

Example 3:

Input: n = 5, buildings = [[1,3],[3,2],[3,3],[3,5],[5,3]]

Output: 1

Explanation:

• Only building [3,3] is covered as it has at least one building:

  <ul>
  	<li>above (<code>[1,3]</code>)</li>
  	<li>below (<code>[5,3]</code>)</li>
  	<li>left (<code>[3,2]</code>)</li>
  	<li>right (<code>[3,5]</code>)</li>
  </ul>
  </li>
  <li>Thus, the count of covered buildings is 1.</li>
  

 

Constraints:

• 2 <= n <= 105
• 1 <= buildings.length <= 105
• buildings[i] = [x, y]
• 1 <= x, y <= n
• All coordinates of buildings are unique.

Solution

---

Python3

class Solution:
    def countCoveredBuildings(self, n: int, buildings: List[List[int]]) -> int:
        rows, cols = len(buildings), len(buildings[0])
        R = defaultdict(list)
        C = defaultdict(list)
        res = 0
 
        for x, y in buildings:
            R[x].append(y)
            C[y].append(x)
 
        for k in R.keys():
            R[k].sort()
 
        for k in C.keys():
            C[k].sort()
 
        for x, y in buildings:
            rIndex = bisect_left(R[x], y)
            cIndex = bisect_left(C[y], x)
 
            if 0 < rIndex < len(R[x]) - 1 and 0 < cIndex < len(C[y]) - 1:
                res += 1
 
        return res