2360. Longest Cycle in a Graph

Problem Link

Description

---

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

 

Example 1:

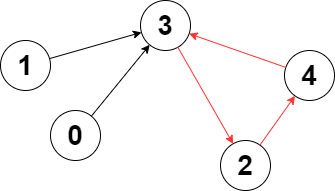
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

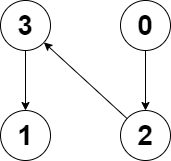
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

Solution

---

Python3

class Solution:
    def longestCycle(self, edges: List[int]) -> int:
        n = len(edges)
        visited = [False] * n
        res = -1
        
        for node in range(n):
            dist = {}
            d = 0
            
            while node != -1 and not visited[node]:
                visited[node] = True
                dist[node] = d
                node = edges[node]
                d += 1
            
            if node != -1 and node in dist:
                res = max(res, d - dist[node])
        
        return res