2718. Sum of Matrix After Queries

Problem Link

Description

---

You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].

Initially, there is a 0-indexed n x n matrix filled with 0's. For each query, you must apply one of the following changes:

• if typei == 0, set the values in the row with indexi to vali, overwriting any previous values.
• if typei == 1, set the values in the column with indexi to vali, overwriting any previous values.

Return the sum of integers in the matrix after all queries are applied.

 

Example 1:

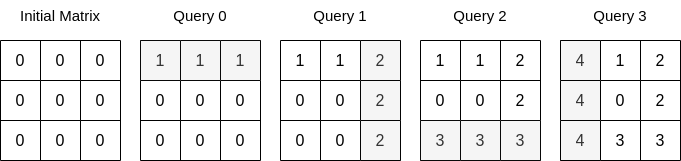
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
Output: 23
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23. 

Example 2:

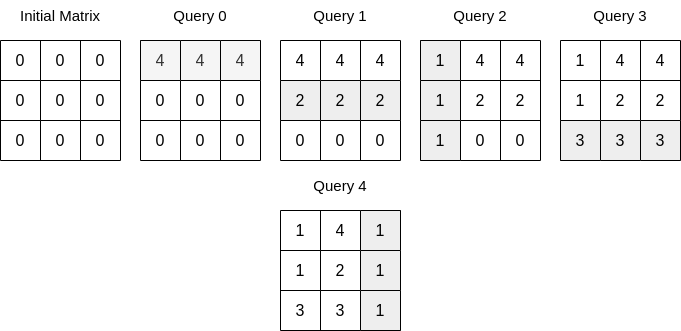
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
Output: 17
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.

 

Constraints:

• 1 <= n <= 104
• 1 <= queries.length <= 5 * 104
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 105

Solution

---

Python3

class Solution:
    def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
        R = defaultdict(tuple)
        C = defaultdict(tuple)
 
        for index, (t, i, value) in enumerate(queries):
            if t == 0:
                R[i] = (index, value)
            elif t == 1:
                C[i] = (index, value)
 
        combined = []
        
        for k, (index, value) in R.items():
            combined.append((index, 0, k, value))
                
        for k, (index, value) in C.items():
            combined.append((index, 1, k, value))
            
        combined.sort(key = lambda x : -x[0])
        rowCount = n
        colCount = n
        res = 0
        
        for _, t, k, value in combined:
            if t == 0:
                res += value * rowCount
                colCount -= 1
            else:
                res += value * colCount
                rowCount -= 1
 
        return res