2116. Check if a Parentheses String Can Be Valid

Problem Link

Description

---

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

• If locked[i] is '1', you cannot change s[i].
• But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can make s a valid parentheses string. Otherwise, return false.

 

Example 1:

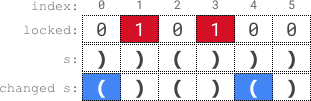
Input: s = "))()))", locked = "010100"
Output: true
Explanation: locked[1] == '1' and locked[3] == '1', so we cannot change s[1] or s[3].
We change s[0] and s[4] to '(' while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = "()()", locked = "0000"
Output: true
Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ")", locked = "0"
Output: false
Explanation: locked permits us to change s[0]. 
Changing s[0] to either '(' or ')' will not make s valid.

Example 4:

Input: s = "(((())(((())", locked = "111111010111"
Output: true
Explanation: locked permits us to change s[6] and s[8]. 
We change s[6] and s[8] to ')' to make s valid.

 

Constraints:

• n == s.length == locked.length
• 1 <= n <= 105
• s[i] is either '(' or ')'.
• locked[i] is either '0' or '1'.

Solution

---

Python3

class Solution:
    def canBeValid(self, s: str, locked: str) -> bool:
        N = len(s)
        s = list(s)
 
        if N & 1: return False
 
        for i in range(N):
            if locked[i] == "0":
                s[i] = "#"
        
        opened = closed = 0
        for x in s:
            if x == "(" or x == "#":
                opened += 1
            else:
                closed += 1
            
            if closed > opened: return False
        
        opened = closed = 0
        for i in range(N - 1, -1, -1):
            if s[i] == ")" or s[i] == "#":
                closed += 1
            else:
                opened += 1
            
            if opened > closed: return False
 
        return True