Description
You are given two integers m and n. Consider an m x n grid where each cell is initially white. You can paint each cell red, green, or blue. All cells must be painted.
Return the number of ways to color the grid with no two adjacent cells having the same color. Since the answer can be very large, return it modulo 109 + 7.
Example 1:

Input: m = 1, n = 1 Output: 3 Explanation: The three possible colorings are shown in the image above.
Example 2:
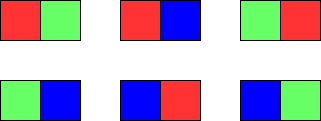
Input: m = 1, n = 2 Output: 6 Explanation: The six possible colorings are shown in the image above.
Example 3:
Input: m = 5, n = 5 Output: 580986
Constraints:
1 <= m <= 51 <= n <= 1000
Solution
Python3
class Solution:
def colorTheGrid(self, m: int, n: int) -> int:
MOD = 10 ** 9 + 7
adj = defaultdict(list)
cols = []
for mask in range(3 ** m):
col = [0] * m
for i in range(m):
col[i] = mask % 3
if i > 0 and col[i] == col[i -1]:
break
mask //= 3
else:
cols.append(tuple(col))
start = tuple([-1] * m) # sentinel
for i in range(len(cols)):
adj[start].append(cols[i])
for j in range(i + 1, len(cols)):
if not any(cols[i][k] == cols[j][k] for k in range(m)): # valid edge
adj[cols[i]].append(cols[j])
adj[cols[j]].append(cols[i])
@cache
def dp(col, pos):
if pos == n:
return 1
count = 0
for nei in adj[col]:
count = (count + dp(nei, pos + 1)) % MOD
return count
return dp(start, 0)