3123. Find Edges in Shortest Paths

Problem Link

Description

---

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

 

Example 1:

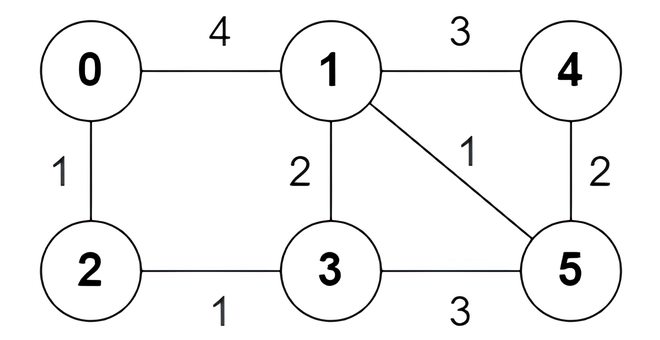
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are all the shortest paths between nodes 0 and 5:

• The path 0 -> 1 -> 5: The sum of weights is 4 + 1 = 5.
• The path 0 -> 2 -> 3 -> 5: The sum of weights is 1 + 1 + 3 = 5.
• The path 0 -> 2 -> 3 -> 1 -> 5: The sum of weights is 1 + 1 + 2 + 1 = 5.

Example 2:

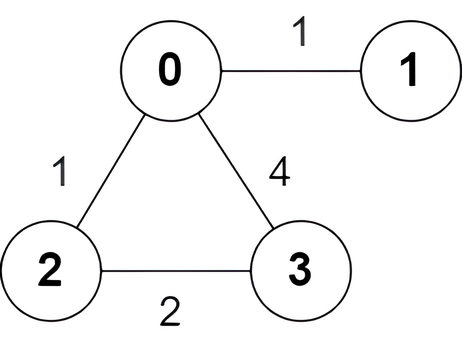
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.

 

Constraints:

• 2 <= n <= 5 * 104
• m == edges.length
• 1 <= m <= min(5 * 104, n * (n - 1) / 2)
• 0 <= ai, bi < n
• ai != bi
• 1 <= wi <= 105
• There are no repeated edges.

Solution

---

Python3

class Solution:
    def findAnswer(self, n: int, edges: List[List[int]]) -> List[bool]:
        M = len(edges)
        graph = defaultdict(list)
 
        for index, (a, b, w) in enumerate(edges):
            graph[a].append((b, w, index))
            graph[b].append((a, w, index))
 
        def dijkstra(n, graph):
            dist = [inf] * n
            parents = defaultdict(list)
            
            pq = [(0, 0)]
            dist[0] = 0
            
            while pq:
                w, node = heappop(pq)
                
                if w != dist[node]: continue
                
                for adj, w2, ei in graph[node]:
                    new = w + w2
                    if new < dist[adj]:
                        dist[adj] = new
                        parents[adj] = [(node, ei)]
                        heappush(pq, (new, adj))
                    elif new == dist[adj]:
                        parents[adj].append((node, ei))
            
            return (dist, parents)
        
        dist, parents = dijkstra(n, graph)
        res = [False] * M
        visited = set()
        
        def go(node):
            if node in visited: return
            
            visited.add(node)
            
            for parent, ei in parents[node]:
                res[ei] = True
                go(parent)
        
        go(n - 1)
        return res