834. Sum of Distances in Tree

Problem Link

Description

---

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

 

Example 1:

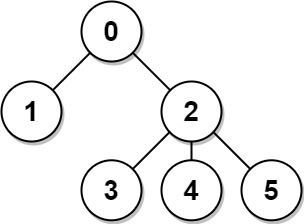
Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

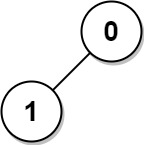
Input: n = 2, edges = [[1,0]]
Output: [1,1]

 

Constraints:

• 1 <= n <= 3 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• The given input represents a valid tree.

Solution

---

Python3

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        graph = defaultdict(list)
 
        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)
        
        count = [0] * n
        res = [0] * n
 
        def dfs(node, prev):
            for adj in graph[node]:
                if adj == prev: continue
 
                dfs(adj, node)
                count[node] += count[adj]
                res[node] += res[adj] + count[adj]
            
            count[node] += 1
        
        def dfs2(node, prev):
            for adj in graph[node]:
                if adj == prev: continue
                # closer -> count[adj] gets 1 closer to the root
                # further -> n - count[adj] gets 1 further to the root
                res[adj] = res[node] - count[adj] + n - count[adj]
                dfs2(adj, node)
 
        
        dfs(0, -1)
        dfs2(0, -1)
 
        return res