1530. Number of Good Leaf Nodes Pairs

Problem Link

Description

---

You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

 

Example 1:

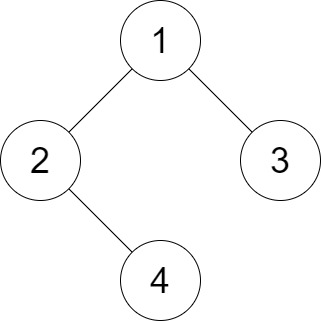
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

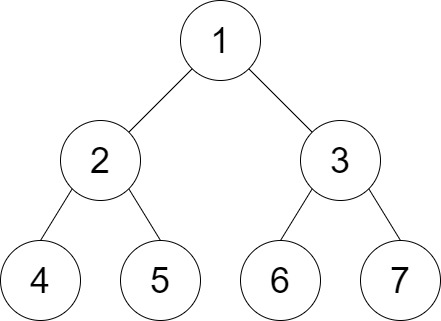
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

 

Constraints:

• The number of nodes in the tree is in the range [1, 210].
• 1 <= Node.val <= 100
• 1 <= distance <= 10

Solution

---

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res;
 
    vector<int> dfs(TreeNode* node, int distance) {
        if (!node) return vector<int>(11, 0);
 
        vector<int> left = dfs(node->left, distance);
        vector<int> right = dfs(node->right, distance);
 
        vector<int> count(11, 0);
 
        if (!node->left && !node->right) {
            count[1] = 1;
            return count;
        }
 
        for (int i = 0; i <= 10; i++) 
            for (int j = 0; j <= 10; j++) 
                if (i + j <= distance) res += (left[i] * right[j]);
            
        for (int i = 0; i <= 9; i++) {
            count[i + 1] += left[i] + right[i];
        }
 
        return count;
    }
 
 
    int countPairs(TreeNode* root, int distance) {
        res = 0;
 
        dfs(root, distance);
 
        return res;
    }
};