1582. Special Positions in a Binary Matrix

Problem Link

Description

---

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

 

Example 1:

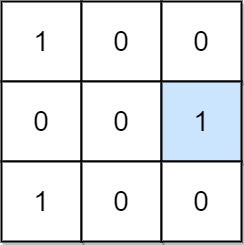
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

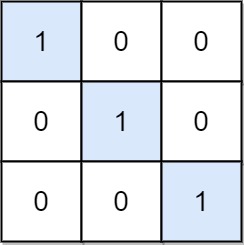
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• mat[i][j] is either 0 or 1.

Solution

---

Python3

class Solution:
    def numSpecial(self, mat: List[List[int]]) -> int:
        rows, cols = len(mat), len(mat[0])
        rowCount = [0] * rows
        colCount = [0] * cols
        res = 0
 
        for i, row in enumerate(mat):
            rowCount[i] = row.count(1)
        
        for i, col in enumerate(zip(*mat)):
            colCount[i] = col.count(1)
        
        for i in range(rows):
            for j in range(cols):
                if mat[i][j] == rowCount[i] == colCount[j] == 1:
                    res += 1
 
        return res