3528. Unit Conversion I

Problem Link

Description

---

There are n types of units indexed from 0 to n - 1. You are given a 2D integer array conversions of length n - 1, where conversions[i] = [sourceUniti, targetUniti, conversionFactori]. This indicates that a single unit of type sourceUniti is equivalent to conversionFactori units of type targetUniti.

Return an array baseUnitConversion of length n, where baseUnitConversion[i] is the number of units of type i equivalent to a single unit of type 0. Since the answer may be large, return each baseUnitConversion[i] modulo 109 + 7.

 

Example 1:

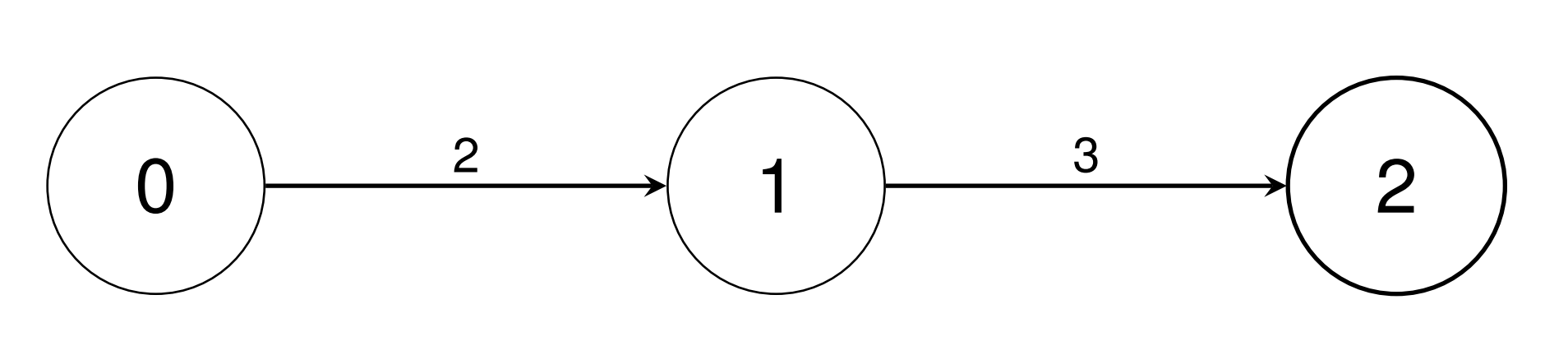
Input: conversions = [[0,1,2],[1,2,3]]

Output: [1,2,6]

Explanation:

• Convert a single unit of type 0 into 2 units of type 1 using conversions[0].
• Convert a single unit of type 0 into 6 units of type 2 using conversions[0], then conversions[1].

Example 2:

Input: conversions = [[0,1,2],[0,2,3],[1,3,4],[1,4,5],[2,5,2],[4,6,3],[5,7,4]]

Output: [1,2,3,8,10,6,30,24]

Explanation:

• Convert a single unit of type 0 into 2 units of type 1 using conversions[0].
• Convert a single unit of type 0 into 3 units of type 2 using conversions[1].
• Convert a single unit of type 0 into 8 units of type 3 using conversions[0], then conversions[2].
• Convert a single unit of type 0 into 10 units of type 4 using conversions[0], then conversions[3].
• Convert a single unit of type 0 into 6 units of type 5 using conversions[1], then conversions[4].
• Convert a single unit of type 0 into 30 units of type 6 using conversions[0], conversions[3], then conversions[5].
• Convert a single unit of type 0 into 24 units of type 7 using conversions[1], conversions[4], then conversions[6].

 

Constraints:

• 2 <= n <= 105
• conversions.length == n - 1
• 0 <= sourceUniti, targetUniti < n
• 1 <= conversionFactori <= 109
• It is guaranteed that unit 0 can be converted into any other unit through a unique combination of conversions without using any conversions in the opposite direction.

Solution

---

Python3

class Solution:
    def baseUnitConversions(self, conversions: List[List[int]]) -> List[int]:
        MOD = 10 ** 9 + 7
        N = len(conversions) + 1
        graph = defaultdict(list)
 
        for x, y, w in conversions:
            graph[x].append((y, w % MOD))
 
        res = [1] * N
 
        def dfs(node, f):
            nonlocal res
 
            res[node] = f
 
            for adj, f2 in graph[node]:
                dfs(adj, (f * f2) % MOD)
 
        dfs(0, 1)
        return res