2946. Matrix Similarity After Cyclic Shifts

Problem Link

Description

---

You are given an m x n integer matrix mat and an integer k. The matrix rows are 0-indexed.

The following proccess happens k times:

• Even-indexed rows (0, 2, 4, ...) are cyclically shifted to the left.

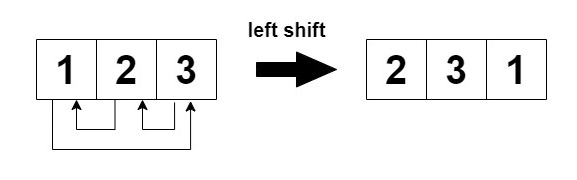
• Odd-indexed rows (1, 3, 5, ...) are cyclically shifted to the right.

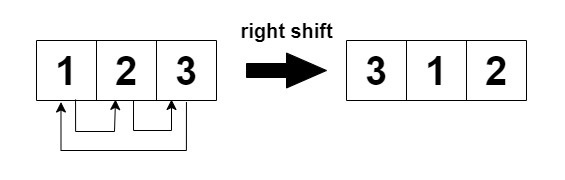
Return true if the final modified matrix after k steps is identical to the original matrix, and false otherwise.

 

Example 1:

Input: mat = [[1,2,3],[4,5,6],[7,8,9]], k = 4

Output: false

Explanation:

In each step left shift is applied to rows 0 and 2 (even indices), and right shift to row 1 (odd index).

Example 2:

Input: mat = [[1,2,1,2],[5,5,5,5],[6,3,6,3]], k = 2

Output: true

Explanation:

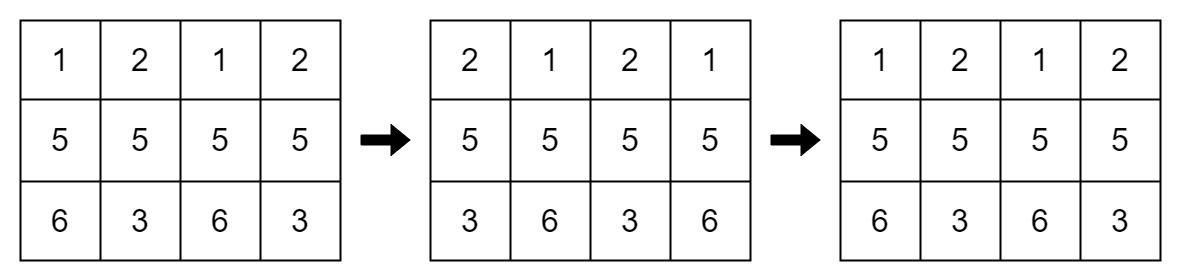
Example 3:

Input: mat = [[2,2],[2,2]], k = 3

Output: true

Explanation:

As all the values are equal in the matrix, even after performing cyclic shifts the matrix will remain the same.

 

Constraints:

• 1 <= mat.length <= 25
• 1 <= mat[i].length <= 25
• 1 <= mat[i][j] <= 25
• 1 <= k <= 50

Solution

---

Python3

class Solution:
    def areSimilar(self, mat: List[List[int]], k: int) -> bool:
        rows, cols = len(mat), len(mat[0])
        
        for row in mat:
            for j in range(cols):
                if row[j] != row[(j + k) % cols]:
                    return False
                
        return True