3515. Shortest Path in a Weighted Tree

Problem Link

Description

---

You are given an integer n and an undirected, weighted tree rooted at node 1 with n nodes numbered from 1 to n. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates an undirected edge from node ui to vi with weight wi.

You are also given a 2D integer array queries of length q, where each queries[i] is either:

• [1, u, v, w'] – Update the weight of the edge between nodes u and v to w', where (u, v) is guaranteed to be an edge present in edges.
• [2, x] – Compute the shortest path distance from the root node 1 to node x.

Return an integer array answer, where answer[i] is the shortest path distance from node 1 to x for the ith query of [2, x].

 

Example 1:

Input: n = 2, edges = [[1,2,7]], queries = [[2,2],[1,1,2,4],[2,2]]

Output: [7,4]

Explanation:

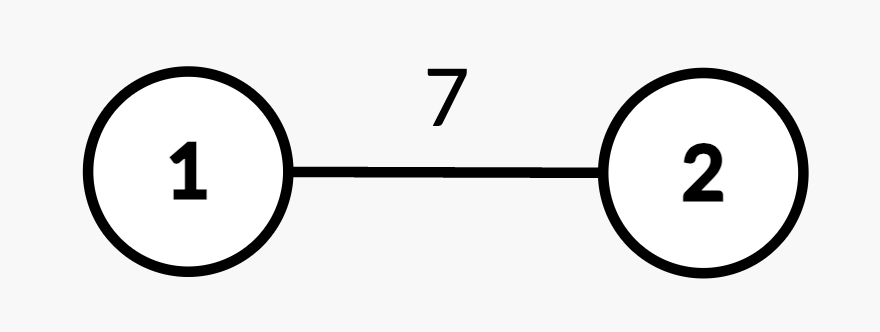
• Query [2,2]: The shortest path from root node 1 to node 2 is 7.
• Query [1,1,2,4]: The weight of edge (1,2) changes from 7 to 4.
• Query [2,2]: The shortest path from root node 1 to node 2 is 4.

Example 2:

Input: n = 3, edges = [[1,2,2],[1,3,4]], queries = [[2,1],[2,3],[1,1,3,7],[2,2],[2,3]]

Output: [0,4,2,7]

Explanation:

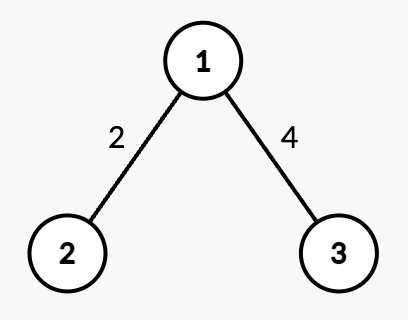
• Query [2,1]: The shortest path from root node 1 to node 1 is 0.
• Query [2,3]: The shortest path from root node 1 to node 3 is 4.
• Query [1,1,3,7]: The weight of edge (1,3) changes from 4 to 7.
• Query [2,2]: The shortest path from root node 1 to node 2 is 2.
• Query [2,3]: The shortest path from root node 1 to node 3 is 7.

Example 3:

Input: n = 4, edges = [[1,2,2],[2,3,1],[3,4,5]], queries = [[2,4],[2,3],[1,2,3,3],[2,2],[2,3]]

Output: [8,3,2,5]

Explanation:

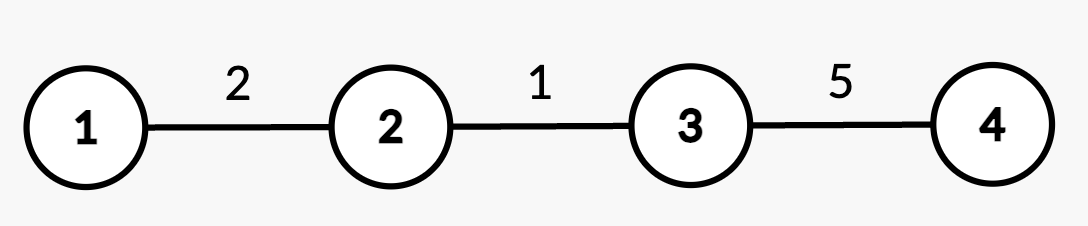
• Query [2,4]: The shortest path from root node 1 to node 4 consists of edges (1,2), (2,3), and (3,4) with weights 2 + 1 + 5 = 8.
• Query [2,3]: The shortest path from root node 1 to node 3 consists of edges (1,2) and (2,3) with weights 2 + 1 = 3.
• Query [1,2,3,3]: The weight of edge (2,3) changes from 1 to 3.
• Query [2,2]: The shortest path from root node 1 to node 2 is 2.
• Query [2,3]: The shortest path from root node 1 to node 3 consists of edges (1,2) and (2,3) with updated weights 2 + 3 = 5.

 

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i] == [ui, vi, wi]
• 1 <= ui, vi <= n
• 1 <= wi <= 104
• The input is generated such that edges represents a valid tree.
• 1 <= queries.length == q <= 105
• queries[i].length == 2 or 4
  • queries[i] == [1, u, v, w'] or,
  • queries[i] == [2, x]
  • 1 <= u, v, x <= n
  • (u, v) is always an edge from edges.
  • 1 <= w' <= 104

Solution

---

Python3

class SegmentTree:
    def __init__(self, arr):
        self.n = len(arr)
        self.tree = [0] * (4 * self.n)
        self.build(1, 0, self.n - 1, arr)
 
    def build(self, v, tl, tr, arr):
        if tl == tr:
            self.tree[v] = arr[tl]
        else:
            tm = tl + (tr - tl) // 2
            self.build(v * 2, tl, tm, arr)
            self.build(v * 2 + 1, tm + 1, tr, arr)
            self.tree[v] = self.tree[v * 2] + self.tree[v * 2 + 1]
 
    def queryHelper(self, l, r):
        return self.query(1, 0, self.n - 1, l, r)
 
    def query(self, v, tl, tr, l, r):
        if l > r: return 0
 
        if tl == l and tr == r:
            return self.tree[v]
        else:
            tm = tl + (tr - tl) // 2
 
        return self.query(v * 2, tl, tm, l, min(tm, r)) + self.query(v * 2 + 1, tm + 1, tr, max(tm + 1, l), r)
    
    def updateHelper(self, pos, value):
        self.update(1, 0, self.n - 1, pos, value)
 
    def update(self, v, tl, tr, pos, value):
        if tl == tr:
            self.tree[v] = value
        else:
            tm = tl + (tr - tl) // 2
 
            if pos <= tm:
                self.update(v * 2, tl, tm, pos, value)
            else:
                self.update(v * 2 + 1, tm + 1, tr, pos, value)
 
            self.tree[v] = self.tree[v * 2] + self.tree[v * 2 + 1]
 
class Solution:
    def treeQueries(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        graph = defaultdict(list)
        for a, b, w in edges:
            graph[a].append((b, w))
            graph[b].append((a, w))
        
        flat_tree = []
        tin = [0] * (n + 1)
        tout = [0] * (n + 1)
 
        def dfs(node, prev, weight):
            flat_tree.append(weight)
            tin[node] = len(flat_tree) - 1
 
            for adj, w2 in graph[node]:
                if adj != prev:
                    dfs(adj, node, w2)
            
            flat_tree.append(-weight)
            tout[node] = len(flat_tree) - 1
        
        dfs(1, -1, 0)
 
        res = []
        st = SegmentTree(flat_tree)
 
        for q in queries:
            if q[0] == 1:
                _, a, b, w = q
                if a > b:
                    a, b = b, a
                node_in, node_out = tin[b], tout[b]
                st.updateHelper(node_in, w)
                st.updateHelper(node_out, -w)
            else:
                node = q[1]
                node_out = tin[node]
                res.append(st.queryHelper(0, node_out))
 
        return res