3615. Longest Palindromic Path in Graph

Problem Link

Description

---

You are given an integer n and an undirected graph with n nodes labeled from 0 to n - 1 and a 2D array edges, where edges[i] = [ui, vi] indicates an edge between nodes ui and vi.

You are also given a string label of length n, where label[i] is the character associated with node i.

You may start at any node and move to any adjacent node, visiting each node at most once.

Return the maximum possible length of a palindrome that can be formed by visiting a set of unique nodes along a valid path.

 

Example 1:

Input: n = 3, edges = [[0,1],[1,2]], label = "aba"

Output: 3

Explanation:

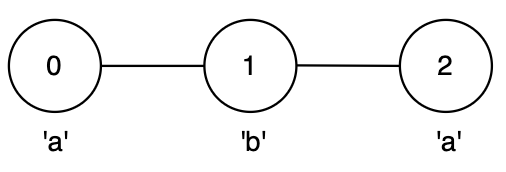
• The longest palindromic path is from node 0 to node 2 via node 1, following the path 0 → 1 → 2 forming string "aba".
• This is a valid palindrome of length 3.

Example 2:

Input: n = 3, edges = [[0,1],[0,2]], label = "abc"

Output: 1

Explanation:

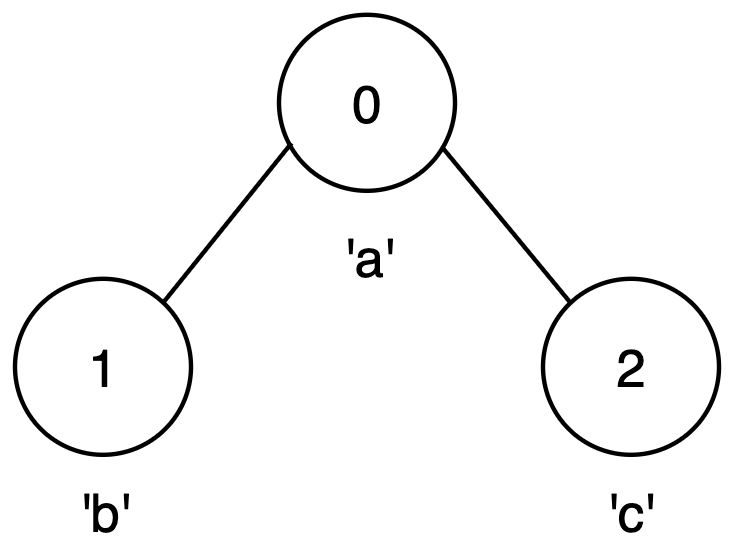
• No path with more than one node forms a palindrome.
• The best option is any single node, giving a palindrome of length 1.

Example 3:

Input: n = 4, edges = [[0,2],[0,3],[3,1]], label = "bbac"

Output: 3

Explanation:

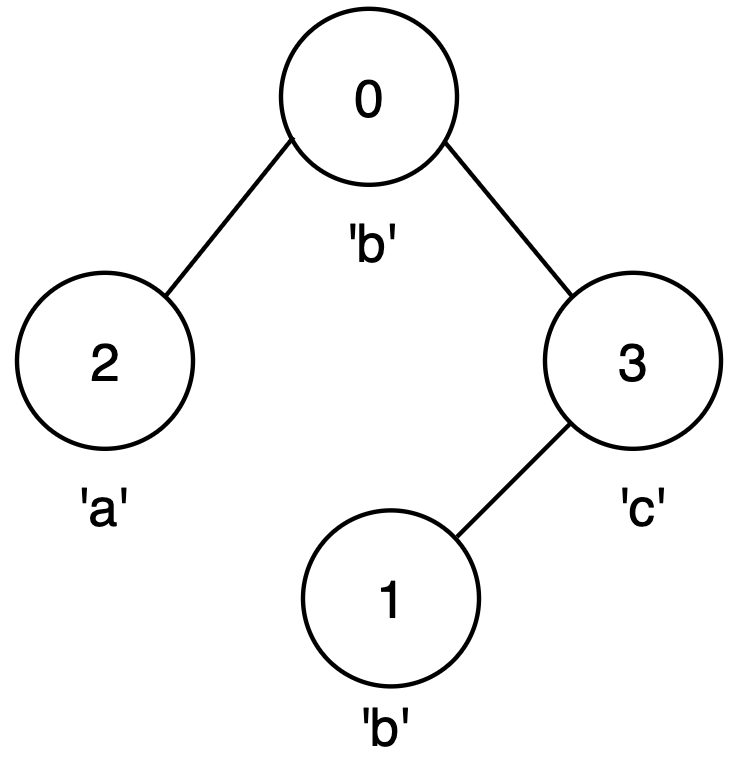
• The longest palindromic path is from node 0 to node 1, following the path 0 → 3 → 1, forming string "bcb".
• This is a valid palindrome of length 3.

 

Constraints:

• 1 <= n <= 14
• n - 1 <= edges.length <= n * (n - 1) / 2
• edges[i] == [ui, vi]
• 0 <= ui, vi <= n - 1
• ui != vi
• label.length == n
• label consists of lowercase English letters.
• There are no duplicate edges.

Solution

---

C++

class Solution {
public:
    static const int MAXN = 14;
    int memo[1 << MAXN][MAXN][MAXN];
 
    int maxLen(int n, vector<vector<int>>& edges, string label) {
        vector<vector<int>> graph(n);
 
        for (const auto& edge : edges) {
            int u = edge[0], v = edge[1];
            graph[u].push_back(v);
            graph[v].push_back(u);
        }
 
        for (int m = 0; m < (1 << n); ++m)
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    memo[m][i][j] = -1;
 
        function<int(int, int, int)> dp = [&](int mask, int u, int v) -> int {
            if (memo[mask][u][v] != -1) return memo[mask][u][v];
 
            int res = 0;
 
            for (int u2 : graph[u]) {
                if (mask & (1 << u2)) continue;
                for (int v2 : graph[v]) {
                    if (u2 == v2) continue;
                    if (mask & (1 << v2)) continue;
                    if (label[u2] != label[v2]) continue;
 
                    int newMask = mask | (1 << u2) | (1 << v2);
                    res = max(res, 1 + dp(newMask, u2, v2));
                }
            }
 
            return memo[mask][u][v] = res;
        };
 
        int res = 1;
 
        // odd-length centers
        for (int node = 0; node < n; ++node) {
            int mask = 1 << node;
            res = max(res, 1 + 2 * dp(mask, node, node));
        }
 
        // even-length centers
        for (const auto& edge : edges) {
            int u = edge[0], v = edge[1];
            if (label[u] != label[v]) continue;
            int mask = (1 << u) | (1 << v);
            res = max(res, 2 * (1 + dp(mask, u, v)));
        }
 
        return res;
    }
};